O (polylog (b))에서 문제를 해결할 수 있습니다.
우리는 f(d, n)n보다 작거나 같은 자릿수를 가진 최대 d 소수 자릿수의 정수로 정의 합니다. 이 함수는 공식에 의해 주어진다는 것을 알 수 있습니다

더 간단한 것으로 시작하여이 함수를 도출해 봅시다.
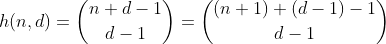
함수 h는 n + 1 개의 다른 요소를 포함하는 다중 세트에서 d-1 개의 요소를 선택하는 방법의 수를 계산합니다. 또한 n을 d 빈으로 분할하는 방법의 수이기도합니다. 이는 n 개의 펜 주위에 d-1 펜스를 만들고 분리 된 각 섹션을 요약하여 쉽게 볼 수 있습니다. n = 2, d = 3 '의 예 :
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
따라서 h는 n과 d의 자릿수 합계를 가진 모든 숫자를 계산합니다. 숫자가 0-9로 제한되므로 10보다 작은 n에 대해서만 작동합니다. 값 10-19에 대해이 문제를 해결하려면 9보다 큰 수를 가진 하나의 빈이있는 파티션 수를 빼야합니다. 이제부터 넘친 빈을 호출합니다.
이 용어는 h를 다음과 같은 방식으로 재사용하여 계산할 수 있습니다. 우리는 n-10을 분할하는 방법의 수를 세고 10을 넣을 빈 중 하나를 선택하여 오버플로 된 빈이 하나 인 파티션 수를 만듭니다. 결과는 다음과 같은 예비 기능입니다.
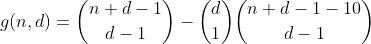
우리는 n-20을 분할하는 모든 방법을 세고 10을 넣을 2 개의 빈을 선택하여 오버 플로우 된 2 개의 빈을 포함하는 파티션 수를 계산하여 n 이하 29에 대해이 방법을 계속합니다.
그러나이 시점에서 우리는 이전 용어에서 2 개의 넘침 된 빈이있는 파티션을 이미 계산 했으므로주의해야합니다. 뿐만 아니라 실제로 두 번 세었습니다. 예를 사용하고 합계 21의 파티션 (10,0,11)을 살펴 보겠습니다. 이전 용어에서 10을 빼고 나머지 11의 모든 파티션을 계산 한 다음 10을 3 개의 빈 중 하나에 넣었습니다. 그러나이 특정 파티션은 다음 두 가지 방법 중 하나로 도달 할 수 있습니다.
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
첫 번째 항에서 이러한 파티션을 한 번 계산 했으므로 오버플로 된 2 개의 빈이있는 파티션의 총 수는 1-2 = -1이되므로 다음 항을 추가하여 한 번 더 계산해야합니다.
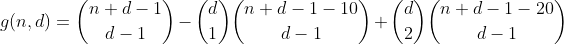
이것에 대해 조금 더 생각하면, 우리는 곧 특정 개수의 오버플로 빈이있는 파티션이 특정 용어로 계산되는 횟수를 다음 표로 표현할 수 있음을 발견했습니다 (열 i는 용어 i를 나타냅니다. 쓰레기통).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
예, 파스칼 삼각형입니다. 우리가 관심을 갖는 유일한 수는 첫 번째 행 / 열에있는 것입니다. 즉, 오버플로 빈이 0 인 파티션의 수입니다. 그리고 모든 행의 교호 합은 첫 행이지만 0과 같으므로 (예 : 1-4 + 6-4 + 1 = 0),이를 제거하고 두 번째 공식에 도달하는 방식입니다.
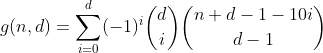
이 함수는 숫자 합이 n 인 d 자리의 모든 숫자를 계산합니다.
자릿수가 n보다 작은 숫자는 어떻습니까? 이항 항에 대한 표준 재발과 귀납적 인수를 사용하여
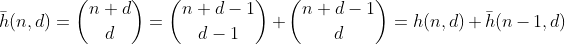
최대 n의 숫자 합계를 갖는 파티션 수를 계산합니다. 그리고이 f에서 g와 같은 인수를 사용하여 도출 할 수 있습니다.
이 공식을 사용하면 예를 들어 8000에서 8999 사이의 간격에서 무거운 수를 찾을 수 있습니다. 1000 - f(3, 20) .이 간격에는 천 개의 숫자가 있기 때문에 28 이하의 숫자 합계를 가진 숫자의 수를 빼야합니다. 첫 번째 숫자는 이미 숫자 합계에 8을 기여한다는 것을 고려합니다.
보다 복잡한 예로 1234..5678 간격의 무거운 숫자를 살펴 보겠습니다. 먼저 1 단계에서 1234에서 1240으로 갈 수 있습니다. 그런 다음 10 단계에서 1240에서 1300으로갑니다. 위의 공식은 각 간격에서 무거운 숫자의 수를 나타냅니다.
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
이제 100 단계로 1300에서 2000으로갑니다.
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
1000 단계로 2000에서 5000까지 :
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
이제 단계 크기를 다시 100 단계로 5000에서 5600으로, 10 단계에서 5600에서 5670으로, 마지막으로 1 단계에서 5670에서 5678으로 단계를 줄여야합니다.
파이썬 구현의 예 (그 동안 약간의 최적화와 테스트를 받았습니다) :
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
편집 : 코드를 최적화 된 버전으로 교체했습니다 (원래 코드보다 더보기 흉한 모양). 내가있는 동안 또한 몇 가지 코너 사례를 수정했습니다. heavy(1234, 100000000)내 컴퓨터에서 약 밀리 초가 걸립니다.
