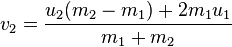볼 투 볼 충돌-감지 및 처리

Stack Overflow 커뮤니티의 도움으로 저는 꽤 기본적이지만 재미있는 물리 시뮬레이터를 작성했습니다.

마우스를 클릭하고 끌어 공을 시작합니다. 튀어 나와 결국 "바닥"에서 멈 춥니 다.

내가 추가하고 싶은 다음 큰 기능은 볼 투 볼 충돌입니다. 공의 움직임은 도끼와 y 속도 벡터로 나뉩니다. 중력 (각 단계마다 y 벡터의 작은 감소)이 있고 마찰이 있습니다 (벽과 충돌 할 때마다 두 벡터의 작은 감소). 공은 놀랍도록 사실적으로 움직입니다.

내 질문에는 두 부분이 있다고 생각합니다.

1. 공 대 공 충돌을 감지하는 가장 좋은 방법은 무엇입니까?
   각 볼을 반복하고 다른 모든 볼을 검사하여 반경이 겹치는 지 확인하는 O (n ^ 2) 루프가 있습니까?
2. 공 대 공 충돌을 처리하기 위해 어떤 방정식을 사용합니까? 물리학 101
   두 개의 볼 속도 x / y 벡터에 어떤 영향을 미칩니 까? 두 개의 볼이 향하는 방향은 무엇입니까? 이것을 각 공에 어떻게 적용합니까?

"벽"의 충돌 탐지 및 결과적인 벡터 변경을 처리하는 것은 쉽지만 볼-볼 충돌과 관련된 더 많은 합병증을 볼 수 있습니다. 벽을 사용하면 적절한 x 또는 y 벡터의 음수를 가져와야 올바른 방향으로 이동합니다. 공으로 나는 그것이 그렇게 생각하지 않습니다.

몇 가지 빠른 설명 : 단순성을 위해 지금은 완벽하게 탄력있는 충돌로 괜찮습니다. 또한 모든 볼은 동일한 질량을 갖지만 앞으로는 변경할 수 있습니다.

편집 : 내가 찾은 자료

벡터가 포함 된 2D 볼 물리학 : Trigonometry가없는 2 차원 충돌 .pdf
2d 볼 충돌 감지 예 : 충돌 감지 추가

성공!

볼 충돌 감지 및 응답이 훌륭하게 작동합니다!

관련 코드 :

충돌 감지 :

for (int i = 0; i < ballCount; i++)  
{  
    for (int j = i + 1; j < ballCount; j++)  
    {  
        if (balls[i].colliding(balls[j]))  
        {
            balls[i].resolveCollision(balls[j]);
        }
    }
}

이것은 모든 공 사이의 충돌을 검사하지만 중복 검사를 건너 뜁니다 (공 1이 공 2와 충돌하는지 확인 해야하는 경우 공 2가 공 1과 충돌하는지 여부를 확인할 필요가 없습니다. 또한 자체 충돌과 충돌 검사를 건너 뜁니다. ).

그런 다음 내 볼 클래스에는 colliding () 및 resolveCollision () 메서드가 있습니다.

public boolean colliding(Ball ball)
{
    float xd = position.getX() - ball.position.getX();
    float yd = position.getY() - ball.position.getY();

    float sumRadius = getRadius() + ball.getRadius();
    float sqrRadius = sumRadius * sumRadius;

    float distSqr = (xd * xd) + (yd * yd);

    if (distSqr <= sqrRadius)
    {
        return true;
    }

    return false;
}

public void resolveCollision(Ball ball)
{
    // get the mtd
    Vector2d delta = (position.subtract(ball.position));
    float d = delta.getLength();
    // minimum translation distance to push balls apart after intersecting
    Vector2d mtd = delta.multiply(((getRadius() + ball.getRadius())-d)/d); 


    // resolve intersection --
    // inverse mass quantities
    float im1 = 1 / getMass(); 
    float im2 = 1 / ball.getMass();

    // push-pull them apart based off their mass
    position = position.add(mtd.multiply(im1 / (im1 + im2)));
    ball.position = ball.position.subtract(mtd.multiply(im2 / (im1 + im2)));

    // impact speed
    Vector2d v = (this.velocity.subtract(ball.velocity));
    float vn = v.dot(mtd.normalize());

    // sphere intersecting but moving away from each other already
    if (vn > 0.0f) return;

    // collision impulse
    float i = (-(1.0f + Constants.restitution) * vn) / (im1 + im2);
    Vector2d impulse = mtd.normalize().multiply(i);

    // change in momentum
    this.velocity = this.velocity.add(impulse.multiply(im1));
    ball.velocity = ball.velocity.subtract(impulse.multiply(im2));

}

소스 코드 : ball to ball collider의 완전한 소스.

누군가이 기본 물리 시뮬레이터를 개선하는 방법에 대한 제안 사항이 있으면 알려주십시오! 아직 추가하지 않은 한 가지는 각도 운동량이므로 볼이 더 사실적으로 굴립니다. 다른 제안? 코멘트를 남겨주세요!

두 개의 공이 충돌하는지 감지하려면 중심 간 거리가 반경의 두 배보다 작은 지 확인하십시오. 볼 사이에서 완전히 탄성 충돌을하려면 충돌 방향의 속도 성분 만 걱정하면됩니다. 다른 구성 요소 (충돌에 접함)는 두 볼 모두 동일하게 유지됩니다. 한 공에서 다른 공으로 방향을 가리키는 단위 벡터를 만든 다음 공의 속도 벡터로 내적을 구하면 충돌 구성 요소를 얻을 수 있습니다. 그런 다음이 구성 요소를 1D 완전 탄성 충돌 방정식에 꽂을 수 있습니다.

Wikipedia는 전체 프로세스에 대해 꽤 좋은 요약을 가지고 있습니다 . 모든 질량의 볼에 대해 새로운 속도는 방정식을 사용하여 계산할 수 있습니다 (여기서 v1 및 v2는 충돌 후 속도, u1, u2는 이전부터).

공의 질량이 동일하면 속도가 간단히 전환됩니다. 다음은 비슷한 코드를 작성하는 코드입니다.

void Simulation::collide(Storage::Iterator a, Storage::Iterator b)
{
    // Check whether there actually was a collision
    if (a == b)
        return;

    Vector collision = a.position() - b.position();
    double distance = collision.length();
    if (distance == 0.0) {              // hack to avoid div by zero
        collision = Vector(1.0, 0.0);
        distance = 1.0;
    }
    if (distance > 1.0)
        return;

    // Get the components of the velocity vectors which are parallel to the collision.
    // The perpendicular component remains the same for both fish
    collision = collision / distance;
    double aci = a.velocity().dot(collision);
    double bci = b.velocity().dot(collision);

    // Solve for the new velocities using the 1-dimensional elastic collision equations.
    // Turns out it's really simple when the masses are the same.
    double acf = bci;
    double bcf = aci;

    // Replace the collision velocity components with the new ones
    a.velocity() += (acf - aci) * collision;
    b.velocity() += (bcf - bci) * collision;
}

효율성에 관해서는 Ryan Fox가 옳습니다. 영역을 섹션으로 나누고 각 섹션에서 충돌 감지를 수행하는 것이 좋습니다. 볼이 섹션의 경계에서 다른 볼과 충돌 할 수 있으므로 코드가 훨씬 복잡해질 수 있습니다. 수백 개의 공을 가질 때까지 효율성은 중요하지 않을 것입니다. 보너스 포인트의 경우 각 섹션을 다른 코어에서 실행하거나 각 섹션 내에서 충돌 처리를 분할 할 수 있습니다.

글쎄, 몇 년 전에 나는 당신이 여기에 제시 한 것과 같은 프로그램을 만들었습니다.
하나의 숨겨진 문제가 있습니다 (또는 다수는 관점에 따라 다름).

• 공의 속도가 너무 빠르면 충돌을 놓칠 수 있습니다.

또한 거의 100 %의 경우 새 속도가 잘못 될 수 있습니다. 글쎄, 속도 가 아니라 위치 . 정확한 위치에서 새로운 속도를 정확하게 계산해야합니다 . 그렇지 않으면 이전의 이산 단계에서 사용할 수있는 약간의 "오류"양으로 볼을 이동시킵니다.

해결책은 분명합니다. 시간 단계를 분리하여 먼저 올바른 장소로 이동 한 다음 충돌 한 다음 남은 시간 동안 이동해야합니다.

이 문제를 해결하려면 공간 분할을 사용해야합니다.

이진 공간 분할 및 쿼드 트리 에 대해 읽어보기

Ryan Fox가 화면을 영역으로 나누고 영역 내 충돌 만 확인하라는 제안을 명확하게 설명합니다.

예를 들어, 플레이 영역을 정사각형 격자로 분할 (각 측면 당 1 단위 길이라고 함) 각 격자 정사각형 내에서 충돌이 있는지 확인합니다.

그것은 절대적으로 올바른 해결책입니다. 다른 포스터가 지적했듯이 그것의 유일한 문제는 경계를 넘어서는 충돌이 문제라는 것입니다.

이에 대한 해결책은 첫 번째 그리드에 0.5 단위의 수직 및 수평 오프셋으로 두 번째 그리드를 오버레이하는 것입니다.

그런 다음 첫 번째 그리드의 경계를 가로 질러 (따라서 감지되지 않은) 충돌은 두 번째 그리드의 그리드 사각형 내에 있습니다. 이미 처리 한 충돌을 추적하는 한 (일부 중복이있을 수 있음) 에지 사례 처리에 대해 걱정할 필요가 없습니다. 모든 충돌은 그리드 중 하나의 그리드 사각형 내에 있습니다.

충돌 검사 횟수를 줄이는 좋은 방법은 화면을 여러 섹션으로 나누는 것입니다. 그런 다음 각 섹션을 같은 섹션의 볼과 비교합니다.

내가 최적화하기 위해 여기에 한 가지가 있습니다.

거리가 반경의 합일 때 공이 맞았 음을 동의하지만 실제로는이 거리를 계산해서는 안됩니다! 오히려 제곱을 계산하고 그 방식으로 작업하십시오. 값 비싼 제곱근 연산에 대한 이유는 없습니다.

또한 충돌을 발견하면 더 이상 남아 있지 않을 때까지 충돌을 계속 평가해야합니다. 문제는 첫 번째 문제는 정확한 그림을 얻기 전에 다른 문제를 해결해야한다는 것입니다. 공이 가장자리에서 공을 때리면 어떻게 될까요? 두 번째 공은 가장자리에 부딪 히고 즉시 첫 번째 공으로 리바운드됩니다. 구석에있는 공 더미에 부딪히면 다음주기를 반복하기 전에 해결해야 할 충돌이 상당히 많을 수 있습니다.

O (n ^ 2)와 관련하여 누락 된 항목을 거부하는 비용을 최소화하기 만하면됩니다.

1) 움직이지 않는 공은 아무것도 칠 수 없습니다. 바닥에 적당한 수의 공이 놓여 있으면 많은 테스트를 저장할 수 있습니다. (정지 된 볼에 무언가가 닿았는지 여전히 확인해야합니다.)

2)해야 할 일 : 화면을 여러 구역으로 나누지 만 선은 흐릿해야합니다. 구역 가장자리의 공은 모든 관련 (4가 될 수 있음) 구역에있는 것으로 표시됩니다. 4x4 그리드를 사용하고 영역을 비트로 저장합니다. 두 볼 구역의 구역의 AND가 0을 반환하면 테스트가 종료됩니다.

3) 내가 언급했듯이, 제곱근을하지 마십시오.

충돌 감지 및 2D 응답에 관한 정보가 담긴 훌륭한 페이지를 발견했습니다.

http://www.metanetsoftware.com/technique.html

그들은 학문적 관점에서 어떻게 수행되는지 설명하려고 노력합니다. 간단한 객체 간 충돌 감지로 시작하여 충돌 대응 및 확장 방법으로 넘어갑니다.

편집 : 업데이트 된 링크

이를 수행하는 두 가지 쉬운 방법이 있습니다. Jay는 공의 중심에서 정확한 점검 방법을 다루었습니다.

가장 쉬운 방법은 사각형 경계 상자를 사용하고 상자 크기를 공 크기의 80 %로 설정하면 충돌을 매우 잘 시뮬레이션 할 수 있습니다.

볼 클래스에 메소드를 추가하십시오.

public Rectangle getBoundingRect()
{
   int ballHeight = (int)Ball.Height * 0.80f;
   int ballWidth = (int)Ball.Width * 0.80f;
   int x = Ball.X - ballWidth / 2;
   int y = Ball.Y - ballHeight / 2;

   return new Rectangle(x,y,ballHeight,ballWidth);
}

그런 다음 루프에서 :

// Checks every ball against every other ball. 
// For best results, split it into quadrants like Ryan suggested. 
// I didn't do that for simplicity here.
for (int i = 0; i < balls.count; i++)
{
    Rectangle r1 = balls[i].getBoundingRect();

    for (int k = 0; k < balls.count; k++)
    {

        if (balls[i] != balls[k])
        {
            Rectangle r2 = balls[k].getBoundingRect();

            if (r1.Intersects(r2))
            {
                 // balls[i] collided with balls[k]
            }
        }
    }
}

나는 여기 저기 힌트를 보았지만 중첩 상자를 비교하는 것과 같이 더 빠른 계산을 먼저 수행 할 수 있으며 첫 번째 테스트가 통과되면 반경 기반 중첩을 수행합니다.

추가 / 차이 수학은 반경에 대한 모든 삼각보다 경계 상자의 경우 훨씬 빠르며, 대부분 경계 상자 테스트는 충돌 가능성을 없애줍니다. 그러나 trig로 다시 테스트하면 원하는 정확한 결과를 얻을 수 있습니다.

예, 두 가지 테스트이지만 전체적으로 더 빠릅니다.

이것은 자바 KineticModel에서 인용 된 접근법 의 구현입니다 .

HTML Canvas 요소를 사용하여 JavaScript로이 코드를 구현했으며 초당 60 프레임으로 멋진 시뮬레이션을 생성했습니다. 무작위 위치와 속도로 12 개의 공을 모아서 시뮬레이션을 시작했습니다. 속도가 높을수록 작은 공과 훨씬 큰 공 사이의 충돌로 인해 작은 공이 큰 공의 가장자리에 달라 붙어 큰 공 주위로 90도 정도 움직여 분리하기 전에 발견되었습니다. (다른 사람 이이 행동을 관찰했는지 궁금합니다.)

일부 계산 결과에 따르면 이러한 경우의 최소 이동 거리는 다음 볼 단계에서 동일한 볼이 충돌하는 것을 방지하기에 충분히 크지 않은 것으로 나타났습니다. 나는 약간의 실험을했고 상대 속도에 따라 MTD를 확장 하여이 문제를 해결할 수 있음을 발견했습니다.

dot_velocity = ball_1.velocity.dot(ball_2.velocity);
mtd_factor = 1. + 0.5 * Math.abs(dot_velocity * Math.sin(collision_angle));
mtd.multplyScalar(mtd_factor);

이 픽스 전후에 충돌 시마다 총 운동 에너지가 보존되었음을 확인했습니다. mtd_factor의 0.5 값은 충돌 후 볼이 항상 분리되도록하는 대략적인 최소값입니다.

이 수정은 시스템의 정확한 물리학에서 약간의 오류를 발생 시키지만, 이제는 시간 단계 크기를 줄이지 않고 브라우저에서 매우 빠른 볼을 시뮬레이션 할 수 있다는 단점이 있습니다.