양자 어닐링을 게이트 모델로 설명 할 수없는 이유는 무엇입니까?

이것은 이 질문을 바탕으로 물어볼 영감을 얻은 것 입니다. 양자 어닐링은 일반적인 회로 모델과 완전히 다른 계산 모델입니다. 나는 이것을 전에 들었고 게이트 모델이 양자 어닐링에 적용되지 않는다는 것을 이해하고 있지만 왜 그런지, 또는 어 닐러가 할 수있는 계산을 구문 분석하는 방법을 이해하지 못했습니다. 몇 가지 대화 (일부 D- 파 자체에 의해)에서 이해할 수 있듯이 어 닐러가 특정 해밀턴에 국한되어 있다는 사실이 그 사실을 이해합니다.

D-Wave 머신과 같은 Quantum Annealer는 Ising 모델을 물리적으로 표현한 것으로 형식의 '문제'Hamiltonian이 있습니다.

본질적으로 해결해야 할 문제는 위의 Hamiltonian에 매핑됩니다. 해밀 토니안의 시스템 시작 어닐링 파라미터 초기 토니안 매핑하는 데 사용된다 문제 해밀 토니안에 사용 입니다.$H_I = \sum_{J=1}^nh'_j\sigma_j^x$$s$$H_I$$H_P$$H\left(s\right) = \left(1-s\right)H_I + sH_P$

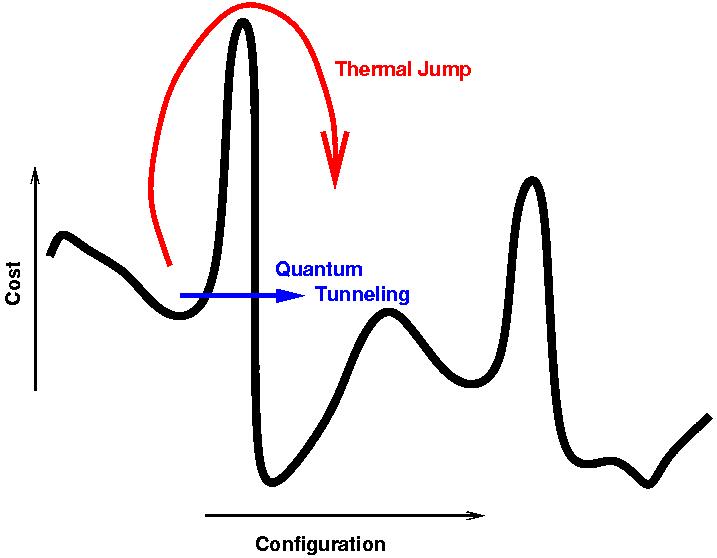
이것은 어닐링이므로 프로세스는 시스템의지면 상태 근처에 머무를 수있을 정도로 느리게 수행되는 반면, 해밀턴 (Hamiltonian)은 Nat의 답변에 설명 된대로지면 상태 근처에 머무르기 위해 터널링을 사용하여 문제에 따라 다양합니다 .

이제 게이트 모델 QC를 설명하는 데 사용할 수없는 이유는 무엇입니까? 위의 내용은 NP-hard 인 2 차 비제 한 이진 최적화 (QUBO) 문제입니다. 실제로, 여기에는 많은 NP 문제를 Ising 모델에 매핑하는 기사가 있습니다 . NP의 모든 문제는 다항식 시간의 모든 NP-hard 문제에 매핑 될 수 있으며 정수 인수 분해는 실제로 NP 문제입니다.

음, 온도는 0이 아니므로 어닐링 전체에 걸쳐지면 상태가되지 않으므로 결과적으로 솔루션은 여전히 ​​근사치입니다. 또는 다른 관점에서, 실패 확률은 절반보다 큽니다 (범용 QC가 '괜찮은'으로 간주하는 것과 비교할 때 적절한 성공 확률을 가진 곳은 거의 없습니다-내가 본 그래프에서 판단하면, 성공 확률은 현재 기계는 약 이며 크기가 커지면 더 나빠질 것입니다.) 및 어닐링 알고리즘은 경계 오류가 아닙니다. 조금도. 따라서 정수 인수 분해와 같은 올바른 솔루션을 가지고 있는지 여부를 알 수있는 방법이 없습니다.$0.2\%$

그것이 원칙적으로하는 것은 정확한 결과에 매우 빠르게 도달하는 것입니다. 그러나 이것은 '거의 정확'에서 '정확한'으로가는 것이 여전히 매우 어려워 정확한 결과가 필요한 곳에 도움이되지 않습니다 ( 즉, '거의 정확한'솔루션을 제공하는 매개 변수가 반드시 매개 변수 근처에있는 위치에 반드시 분배 될 필요는 없기 때문에,이 경우에 원래의 문제가 NP에있을 때 일반적으로 여전히 NP 일 수있다. 올바른 해결책.

설명을 위해 편집 : 이것은 의미 QA (quantum annealer)가 정수 인수 분해와 같은 NP 문제를 해결하기 위해 여전히 지수 시간 (잠재적으로 빠른 지수 시간이 소요됨)을 취한다는 것입니다. 일반 QC는 지수 속도를 높이고 동일한 많은 시간에 문제가 있습니다. 이것이 QA가 폴리 타임으로 범용 QC를 시뮬레이션 할 수 없다는 것을 의미합니다 (그렇지 않으면 폴리 타임에서 해결할 수없는 문제를 해결할 수 있음). 코멘트에 지적이는 없습니다 품질 보증은 데이터베이스 검색과 같은 다른 문제에서 같은 속도 향상을 줄 수 없다는 같은.

어닐링은 아날로그 전술에 가깝습니다.

요점은 최적화하려는 이상한 기능이 있다는 것입니다. 그래서, 당신은 그 주위에 튀어 오릅니다. 처음에는 " 온도 "가 매우 높아서 선택한 지점이 많이 튀어 오를 수 있습니다. 그런 다음 알고리즘이 " 냉각 "되면 온도가 내려 가고 바운싱이 덜 공격적입니다.

궁극적으로, 그것은 최적의 글로벌 옵티마와 같은 로컬 옵티마에 정착합니다.

시뮬레이션 어닐링 (비 양자)에 대한 애니메이션은 다음과 같습니다 .

그러나 양자 어닐링 과 거의 같은 개념입니다 .

대조적으로, 게이트 로직은 아날로그보다 훨씬 더 디지털입니다. 혼란스러운 바운스 후 단순히 결과를 찾는 것이 아니라 큐 비트 및 논리 연산과 관련이 있습니다.