블로흐 구체에서 Z 게이트에 대해 생각하는 방법?

이해하는 방법에 대해 혼란스러워합니다. $Z$ Bloch 구체에있는 문.

매트릭스를 고려 $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ 이해할 수있다 $Z|0\rangle = |0\rangle$ 과 $Z|1\rangle = -|1\rangle$.

그것은 설명 여기에 그$Z$ 게이트는 $\pi$ 주위 회전 $Z$중심선. 그럼 어떻게 이해해야합니까$Z|1\rangle = -|1\rangle$? 이후$|1\rangle$ 남극이라고 생각합니다. $\pi$ 주위 회전 $Z$ 축은 아무것도하지 않습니다.

블로흐 구체에 대해 생각하는 방식은 상태의 밀도 매트릭스와 관련이 있습니다. $Z$ 에 행동 $|0\rangle\langle 0|$ 또는 $|1\rangle\langle 1|$대각선 밀도 행렬의 경우와 마찬가지로 아무 것도 수행하지 않습니다. 회전의 효과를 보려면 비대 각 밀도 행렬이$Z$와 같은 $|+\rangle\langle +|$.

$|1\rangle$ 과 $-|1\rangle$Bloch 구체의 동일한 점에 전역 위상 이 같기 때문에 동일한 점에 지정됩니다 . 대수적으로 :$|1\rangle \equiv -|1\rangle$ 어디 $\equiv$"전세계 단계와 동일"을 의미합니다. 의미하는 것은$\theta$ 그런 $-|1\rangle = e^{i \theta} |1\rangle$.

당신을 혼란스럽게하는 것은 $|0\rangle \equiv Z |0\rangle$ 과 $|1\rangle \equiv Z |1\rangle$이 둘의 선형 조합에는 적용되지 않습니다. 예를 들어$Z |+\rangle \not\equiv Z |+\rangle$ 비록 $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$.

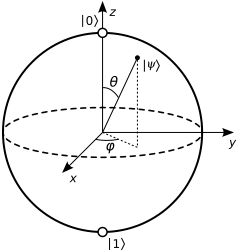
Wikipedia에 따라 순수한 상태를 다음과 같이 작성할 수 있습니다.

$$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$$

어디 $\theta$ 과 $\phi$ 블로흐 구체의 각도는 다음과 같습니다.

표면의 거의 모든 점 (즉, 순수한 상태)은 극점을 제외하고 각도로 독특한 표현을합니다. 지구와 마찬가지로 남극에는 경도가 정의되어 있지 않습니다 (모든 경도가 동일하게 작동 함).$|1 \rangle$ 모든 단계를 진술하다 $\phi$같은 것을 의미합니다. “위도”$\theta$ 여기에 $\pi$이를 방정식에 연결해 봅시다.

$$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$$ $$= 0 + e^{i \phi} |1 \rangle$$

오일러의 정체성에 익숙하다면 아마 $e^{i \phi}$복잡한 평면에서의 회전으로 특히, 이후$Z$ 에 대한 회전입니다 $\phi = \pi$우리는 유명해집니다 $e^{i \pi} = -1$, 마침내 도착 $|1 \rangle = - |1 \rangle$.