가장 모호한 정렬 알고리즘은 무엇입니까? [닫은]

방금 sortvis.org 블로그 게시물을 통해 cyclesort 에 대해 읽었 습니다. 이것은 내가 지금까지 들어 본 것 중 가장 모호한 것입니다. 왜냐하면 익숙하지 않은 수학을 사용하기 때문입니다 (정수 세트의 순열에서주기를 감지).

가장 모호한 것이 무엇입니까?

인내 정렬에 대해 들어 본 적이 있습니까? 이제는 ...

Slowsort 는 나누고 정복하는 것이 아니라 곱셈과 항복으로 작동합니다. 그것은 아마도 가장 효율적으로 구축 될 수있는 가장 효율적인 정렬 알고리즘이기 때문에 흥미 롭습니다.

최상의 경우 bogosort는 매우 효율적으로, 즉 어레이가 이미 정렬 된 경우 bogosort에서 상쇄됩니다. Slowsort는 그러한 최고의 행동으로부터 "고통"하지 않습니다. 가장 좋은 경우에도 여전히 ϵ > 0의 런타임 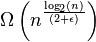이 있습니다.

다음은 독일 위키피디아 기사 에서 수정 한 의사 코드입니다 .

function slowsort(A, i, j):
  if i >= j: return

  m = (i + j) / 2
  slowsort(A, i, m)
  slowsort(A, m + 1, j)

  if A[j] < A[m]:
    swap(A[j], A[m])

  slowsort(A, i, j - 1)

이것이 모호한 것으로 간주되는지 모르겠지만 가장 어리석은 정렬 "알고리즘"중 하나는 Bogosort 입니다. Bogosort 페이지의 링크도 재미 있습니다.

그리고 "quantum bogo-sort"섹션에서이 보석이 있습니다.

^2N 유니버스를 만드는 것도 메모리를 많이 사용합니다.

흠 ... 당신은 말할 수 있습니다 :-).

또 다른 모호한 "알고리즘"은 Intelligent Design Sort 이지만 알고리즘이 빠르거나 메모리 소비가 적습니다. :)

수면 정렬 은 다소 참신합니다.

    #!/bin/bash
    function f() {
        sleep "$1"
        echo "$1"
    }
    while [ -n "$1" ]
    do
        f "$1" &
        shift
    done
    wait

사용법 예 :

    ./sleepsort.bash 5 3 6 3 6 3 1 4 7

이 상황에서도 거품 정렬이 잘못된 대답이라고 생각합니다.

:)

연습 중 하나에 대한 답변으로 Knuth Volume 3 ¹ 은 기본적으로 고대 코드 골프 인 이름없는 정렬 알고리즘을 구현합니다. MIX 어셈블리 언어로 작성할 수있는 가장 짧은 정렬입니다. 짧은 코드는 O (N ³ ) 복잡성의 최저 가격으로 제공됩니다 ...

¹ 적어도 구판. 새 버전에 대한 MIXAL의 수정 사항을 감안할 때 여전히 MIXAL이 있는지 또는 확실하지 않은지 MIXAL이 원래 MIXAL에 있는지 여부는 확실하지 않습니다.

내 데이터 구조 클래스에서 Stooge sort 의 정확성을 명시 적으로 증명해야했습니다 . 실행 시간은 O (n ^ {log 3 / log 1.5}) = O (n ^ 2.7095 ...)입니다.

그것이 가장 모호한 지 모르겠지만 스파게티 종류 는 그것을 사용할 수있는 상황에서 최고 중 하나입니다.

원본 Knuth 서적 중 하나 인 "정렬 및 검색"에는 하드 디스크를 사용하지 않고 테이프 파일을 정렬하는 프로세스를 나타내는 중간 단계가 있습니다. 필자는 6 개의 테이프 드라이브를 사용했으며 각 드라이브가 앞으로 읽기, 뒤로 읽기, 되감기 또는 유휴 상태 일 때 명시 적으로 표시했다고 생각합니다. 오늘날 그것은 쓸모없는 기술의 기념비입니다.

한 번 CRAY 어셈블러에서 벡터 레지스터 거품 정렬을 수행했습니다. 기계에는 이중 이동 명령이있어서 벡터 레지스터의 내용을 한 단어 씩 위 / 아래로 이동할 수 있습니다. 다른 모든 지점을 두 개의 벡터 레지스터에 넣으면 완료 될 때까지 다른 메모리 참조를 만들지 않고도 완전한 버블 정렬을 수행 할 수 있습니다. 거품 정렬의 N ** 2 특성을 제외하고는 효율적이었습니다.

또한 한 번의 정렬을 위해 가능한 한 빨리 길이 4 벡터의 부동 소수점 정렬을 수행해야했습니다. 테이블 조회 (A2-A1의 부호 비트는 하나의 비트, A3-A1의 부호는 다른 비트를 형성합니다 ...)를 사용하여 테이블에서 순열 벡터를 찾습니다. 실제로 내가 올 수있는 가장 빠른 솔루션이었습니다. 현대식 아키텍처에서는 잘 작동하지 않지만 부동 및 정수 단위는 너무 분리되어 있습니다.

Google 코드 잼에는 Gorosort라는 알고리즘에 대한 문제가 있었으며 문제를 위해 발명했다고 생각합니다.

Goro에는 4 개의 무기가 있습니다. 고로는 매우 강하다. 당신은 Goro를 망칠 필요가 없습니다. Goro는 N 개의 다른 정수 배열을 정렬해야합니다. 알고리즘은 Goro의 힘이 아닙니다. 힘은 Goro의 힘입니다. Goro의 계획은 두 손으로 손가락을 사용하여 배열의 여러 요소를 잡고 가능한 한 세 번째와 네 번째 주먹으로 테이블을 때리는 것입니다. 그러면 어레이의 보안되지 않은 요소가 공중으로 날아가 무작위로 섞여 빈 어레이 위치로 넘어갑니다.

http://code.google.com/codejam/contest/dashboard?c=975485#s=p3

이름은 기억하지 않지만 기본적으로

while Array not sorted

  rearrange the array in a random order

쉘 정렬

알고리즘 자체가 그다지 모호하지는 않지만 실제로 실제로 사용되는 구현의 이름을 누가 지정할 수 있습니까? 제가 할수 있어요!

TIGCC (TI-89 / 92 / V200 그래프 계산기 용 GCC 기반 컴파일러)는 qsort표준 라이브러리에서 구현을 위해 셸 정렬을 사용 합니다.

__ATTR_LIB_C__ void qsort(void *list, short num_items, short size, compare_t cmp_func)
{
  unsigned short gap,byte_gap,i,j;                
  char *p,*a,*b,temp;                       
  for (gap=((unsigned short)num_items)>>1; gap>0; gap>>=1)    // Yes, this is not a quicksort,
    {                                                         // but works fast enough...    
      byte_gap=gap*(unsigned short)size;
      for(i=byte_gap; i<((unsigned short)num_items)*(unsigned short)size; i+=size)
        for(p=(char*)list+i-byte_gap; p>=(char*)list; p-= byte_gap)
          {
            a=p; b=p+byte_gap;
            if(cmp_func(a,b)<=0) break;
            for(j=size;j;j--)
              temp=*a, *a++=*b, *b++=temp;
          }
    }
}

코드 크기를 작게 유지하기 위해 퀵 정렬을 위해 셸 정렬을 선택했습니다. 점근 적 복잡성이 더 나쁘지만 TI-89는 RAM이 많지 않습니다 (190K, 프로그램 크기 및 아카이브되지 않은 변수의 총 크기). 따라서 항목 수는 낮다.

내가 작성한 프로그램에서 너무 느리다고 불평 한 후에 더 빠른 구현이 작성되었습니다. 어셈블리 최적화와 함께 더 나은 간격 크기를 사용합니다. qsort.c 에서 찾을 수 있습니다.