PCA 플롯의 쐐기 모양은 무엇을 나타 냅니까?

이들에는 텍스트 분류 autoencoders 종이 힌튼 및 Salakhutdinov (PCA 밀접한 관련이있다) 2 차원 LSA 제조 플롯을 보여 주었다 : .

전혀 다른 약간 높은 차원의 데이터에 PCA를 적용하면 비슷한 모양의 플롯을 얻었습니다 (이 경우를 제외하고 내부 구조가 있는지 정말로 알고 싶었습니다).

임의의 데이터를 PCA에 공급하면 디스크 모양의 얼룩을 얻으므로이 쐐기 모양의 모양은 무작위가 아닙니다. 그 자체로 무엇을 의미합니까?

변수가 양수 또는 음수라고 가정 할 때 모서리의 가장자리는 데이터가 각각 0 또는 음수가되는 지점 일뿐입니다. 이러한 실제 데이터가 오른쪽으로 치우친 경향이 있기 때문에 분포의 최하위에서 더 높은 점 밀도와 쐐기의 "점"에서 더 큰 밀도를 볼 수 있습니다.

보다 일반적으로, PCA는 단순히 데이터의 회전이며 이러한 데이터에 대한 제약 조건은 일반적으로 질문에 표시된 것과 동일한 방식으로 주요 구성 요소에서 볼 수 있습니다.

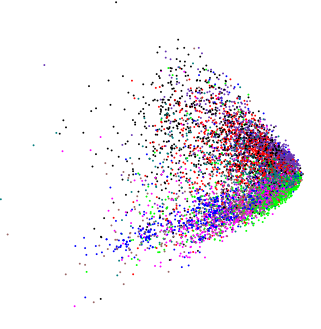
다음은 여러 로그 정규 분포 변수를 사용하는 예입니다.

library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

처음 두 PC를 암시 회전에 따라, 당신은 쐐기를 볼 수 있습니다 또는 약간 다른 버전을 볼 수 있습니다 (사용 차원에서 여기에 표시 ordirgl()대신에 plot())

여기서, 3d에서 우리는 중심 질량에서 여러 개의 스파이크가 튀어 나오는 것을 볼 수 있습니다.

가우스 랜덤 변수 ( ) 각각에 대해 동일한 평균과 분산을 갖는 점의 구체$X_i \sim \mathcal(N)(\mu = 0, \sigma = 1)$

set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")

균일 한 양의 랜덤 변수의 경우 큐브가 보입니다.

set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")

여기서는 설명을 위해 3 개의 임의 변수를 사용하여 유니폼을 표시하므로 점은 3d의 큐브를 나타냅니다. 더 큰 치수 / 더 많은 변수를 사용하면 5D 하이퍼 큐브를 3D로 완벽하게 표현할 수 없으므로 뚜렷한 "큐브"모양이 다소 왜곡됩니다. 비슷한 문제가 표시된 다른 예에 영향을 주지만 해당 예의 제약 조건을 여전히 쉽게 확인할 수 있습니다.

데이터의 경우 PCA 이전의 변수에 대한 로그 변환은 선형 회귀 분석에서 이러한 변환을 사용할 수있는 것처럼 꼬리를 잡아 당겨 덩어리 데이터를 확장합니다.

다른 모양은 PCA 플롯에서 잘릴 수 있습니다. 이러한 형태 중 하나는 PCA에 보존 된 메트릭 표현의 인공물이며 말굽으로 알려져 있습니다. 길거나 지배적 인 그래디언트가있는 데이터의 경우 (변수가 0에서 최대로 증가한 다음 데이터의 일부를 따라 다시 0으로 감소하는 단일 차원을 따라 배열 된 샘플은 이러한 인공물을 생성하는 것으로 잘 알려져 있습니다.)

ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
                 Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
                 Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
        ylab = "Abundance", xlab = "Sites")

축 끝의 점이 가운데로 구부러지는 극단적 인 말굽을 생성합니다.