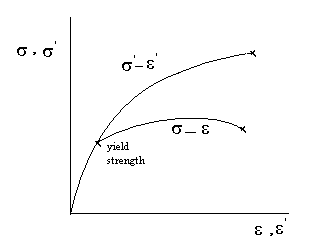우리는 왜 엔지니어링 스트레스를 사용합니까?

놀랍게도 이것은 이전에 요청되지 않았으므로 간단한 것을 놓치고 있어야합니다.

우리는이 방정식에서 엔지니어링 스트레스와 엔지니어링 변형을 사용합니다. 응력 = (영률) × (변형). 이 등식 굽힘 빔, 비틀림 샤프트 및 좌굴 해석에 사용됩니다. 휨의 최종 식도록 과 비틀림 줄 것이다 우리는 공학적 스트레스의 가치는 있지만 스트레스의 가치는 아닙니다.$(\frac{M}{I} = \frac{\sigma}{y})$$(\frac{T}{I} = \frac{\tau}{r})$

우리는 왜 정확한 응력 값을 줄 수 없다는 것을 알면서도 실제 응력 대신 공학 스트레스를 고려하고 있습니까?

내가 읽는 것들은 다음과 같습니다.

1. 측정하기 어려움.
2. 그다지 큰 차이는 없으며 안전 계수를 적용 할 수 있습니다.
3. "우리는 소성 변형을 갖지 않도록 설계하기 때문에 탄성 영역이 가장 중요하므로 비례 한계가 중요하지 않은 경우에 발생하는 현상 때문에 로딩 후 재료의 단면적을 변경하는 것을 고려하지 않습니다."

첫째, 1과 2는 나에게 진정한 이유가 아닙니다. 우리는 항상 탄성 영역에서 디자인하기 때문에 3 번은 그럴듯 해 보이지만 이것이 맞습니까? 엔지니어링 스트레인은 비례 제한 이후에도 유효한 정보를 제공합니까?

대부분의 경우, 특히 탄성 영역에서 엔지니어링 변형이 실제 변형과 무시할 수 있기 때문에 "올바른"값이 아니지만 엔지니어링 변형을 사용합니다.

직선 탄성, Hookean 재료의 경우, 일반적으로 탄성 한계에서의 변형이 매우 작은 경우입니다. 예를 들어 가장 강한 강재의 경우에도 냉간 가공시 약 있습니다. 강철의 계수는 대략 입니다. 따라서 가장 강한 강재의 경우 입니다. 따라서 소성 변형이 시작될 때 엔지니어링 변형률은 입니다. 많은 유용한 탄성 재료는 탄성 한계에서 엔지니어링 변형이 훨씬 낮습니다.$\sigma_{\textrm{el}}=1\times 10^{9}\ \textrm{Pa}$$E=200\times 10^{9}\ \textrm{Pa}$$\varepsilon_{\textrm{el}}=0.005=0.5\%$$0.5\%$

등방성, Hookean 탄성체의 경우 다음과 같습니다.

$$\varepsilon_{x_{1}} = \frac{1}{E}\left[\sigma_{x_{1}}-\nu\left(\sigma_{x_{2}}+\sigma_{x_{3}}\right)\right]$$

선택에서 일반성을 잃지 않고 . 따라서 탄성 한계에서의 단축 장력에서 재료가 자유롭게 수축한다고 가정하면 σ x 2 = σ x 3 = 0 입니다. 따라서 ε x 2 = ε x 3 = − σ el$x_{i}$$\sigma_{x_{2}}=\sigma_{x_{3}}=0$. 탄성 영역에서 강의포아송 비ν는 대략 0.3이기 때문에,단면 선형 압축 변형률은0.0015이다. 탄성 한계에서의 단면적이며, 따라서(1-0.0015)20또는 아주 가까운0.997배 원래 영역.$\varepsilon_{x_{2}}=\varepsilon_{x_{3}}=-\frac{\sigma_{\textrm{el}}\nu}{E}=-\nu\varepsilon_{\textrm{el}}$$\nu$$0.0015$$(1-0.0015)^{2}A_{0}$$0.997$

따라서 진정한 변형은 $\frac{1}{0.997}$$1.003$$0.3\%$

상기 분석은 선형 탄성의 Hookean 고체에 합리적으로 유용하지만, 중합체 및 생물학적 재료에 대해서는 잘 유지되지 않는다. 이러한 재료는 일반적으로 점탄성 (또는 다른 종류의 재료)이므로 동작에 따라 다른 규칙을 따릅니다. 다음 그래프에서 알 수 있듯이 진정한 변형도, 플라스틱 정권에 엔지니어링 균주로부터 매우 격렬하게 발산 (찾을 여기에 )

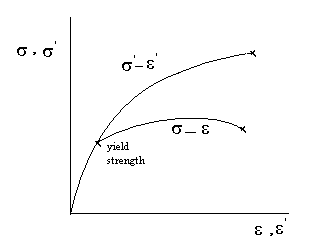
당신의 요점에 관해서 :

1. 변형 중 단면적의 변화를 측정하는 것은 어렵습니다. 정밀하게 가공 된 테스트 샘플에 보정 된 계측기를 신중하게 배치해야합니다. 인장 시험 장비 에서 단축 인장 및 압축에서의 측면 변형을 측정하기 위해 인장 막대 의 측면에 배치 된 스트레인 게이지를 사용할 수 있습니다 . 통계적으로 의미있는 결과를 얻으려면 많은 시간과 노력 및 비용뿐만 아니라 많은 샘플이 필요합니다.

2. $0.3\%$

3. 우리가 탄력 체제의 끝을 넘어서는 무엇이든 무시할 수 있거나 항상 탄력 체제를 위해 설계한다는 생각은 사실이 아닙니다. 소성 변형은 종종 연구 할 가치가 있습니다. 롤링, 드로잉, 압출 등과 같은 연속적인 형상 형성 공정을 모델링하려면 소성 변형 역학에 대한 깊은 이해가 필요하며,이를 위해서는 진정한 응력과 진정한 변형이 중요합니다. 소성 변형은 충돌 중 차체 패널 및 프레임 구성 요소와 같이 일부 예상 사용 사례에서 영구적으로 변형되어야하는 재료 모델링에도 유용합니다 (도면 pdf 참조 ). 소성 변형은 운동 에너지를 흡수하기 때문에 유용합니다.

편집 : 사과합니다. 실제로 스트레스에 대한 질문에 대답하지 않았습니다. 그러나 탄성 영역에서의 선형 관계가 주어지면 변형에 적용되는 것과 동일한 점이 응력에 적용된다는 것이 상당히 분명해야합니다. 다시 한 번, 소성 체제에서는 큰 변화가있을 수 있습니다.

@starrise의 답변에 추가 :

이유 1과 2의 해고와 관련하여, 당신은 그에 관한 비용-이익 분석을 고려하는 것을 잊고 있습니다. @starrise가 그들의 답변에서 알 수 있듯이, 그 차이는 일반적으로 크지 않습니다 (다른 재료는 일반적으로 더 큰 차이를 갖지만).

$\pm6\%$ $\pm15\%$

따라서 다른 모든 특성 (항복 강도 및 단면 치수 포함)이 사용으로 인해 "오류"를 익히지 않는 임의의 변동이 발생하는 경우 일상적인 엔지니어링 실무에서 실제 변형을 고려하는 시점은 무엇입니까? 진정한 스트레인 대신 엔지니어링 스트레인?