베이 즈 정리는 무엇에 관한 것입니까?

베이 즈 정리 와 관련된 주요 아이디어, 즉 개념은 무엇입니까 ? 복잡한 수학 표기법의 파생을 요구하지 않습니다.

베이 즈 정리는 비교적 단순하지만 특정 조건부 확률의 계산을 허용하는 확률 이론의 기본 결과입니다. 조건부 확률은 한 사건이 다른 사건의 확률에 미치는 영향을 반영하는 확률입니다.

간단히 말해서, 가장 유명한 형태로, 새로운 데이터에 대한 가설의 확률 ( P (H | D) ; 사후 확률이라고 함)은 다음 방정식과 같다고 가정합니다. 가설에 따른 관측 된 데이터의 확률 ( P (D | H) ; 조건부 확률이라고 함), 새로운 증거 이전에 이론 확률이 참인 시간 ( P (H) ; H 의 사전 확률이라고 함)을 해당 데이터를 볼 확률로 나눈 기간 ( P (D ); D 의 한계 확률이라고합니다.

공식적으로 방정식은 다음과 같습니다.

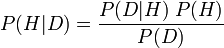
베이 즈 정리의 중요성은 대체로 가능성에 대한 생각의 학교들 사이에서 논쟁의 지점이되기 때문에 적절한 사용으로 인한 것입니다. 주관적 베이지안 (확률을 주관적 신념 도로 해석하는)에게 베이 즈 정리는 주관적 확률 판단을 방정식에 꽂고 그것과 함께 실행함으로써 이론 테스트, 이론 선택 및 기타 관행의 초석을 제공합니다. ( 빈도를 상대 주파수 를 제한 하는 것으로 해석하는) 잦은 주의자에게, 베이 즈 정리의 이러한 사용은 남용이며, 대신 (또 다른 확률 해석의 객관적인 베이지 안에서와 같이) 의미있는 (비 주관적인) 선행을 사용하려고 노력합니다.

미안하지만 혼란 스러울 것 같습니다. 베이 즈 정리는 끝없는 베이 즈- 자주주의 토론에 대한 논의를 위해 있지 않습니다 . 두 생각의 학교와 일치하는 정리입니다 (Kolmogorov의 확률 공리와 일치하는 경우).

물론 베이 즈 정리는 베이 즈 통계의 핵심이지만 정리 자체는 보편적입니다. 잦은 주의자와 베이지안 사이의 충돌은 주로 이전 분포를 정의 할 수있는 방법과 관련이 있습니다.

따라서 질문이 베이 즈 정리 (베이지 통계가 아님)에 관한 것이라면 :

베이 즈 정리는 특정 조건부 확률을 계산할 수있는 방법을 정의합니다. 예를 들어, 누군가가 질병 X를 가지고 있다고 가정 할 때 누군가 증상 A를 가질 가능성이 있다고 상상해보십시오. p (A | X); 일반적으로 질병 X p (X)를 갖는 누군가의 확률; 일반적으로 누군가 증상 Ap (A)를 가질 확률. 이 3 가지 정보를 사용하면 증상 A p (X | A)를 가진 사람이 질병 X에 걸릴 확률을 계산할 수 있습니다.

베이 즈 정리는 조건부 확률 를 다른 조건부 확률 로 회전시키는 방법 입니다.$P(A|B)$$P(B|A)$

일부의 걸림돌은 의 의미입니다 . 이것은 반드시 발생하는 (또는 사실 인) 이벤트 만 고려하여 가능한 이벤트의 공간을 줄이는 방법 입니다. 예를 들어, 6 ( 나타내는 던지고 공정한 주사위 땅 이있을 확률은 1/6이지만 짝수 인 은 1/3입니다.$P(B|A)$$A$$P(\mbox{dice lands six})$$P(\mbox{dice lands six}|\mbox{dice lands even})$

베이 즈 정리를 다음과 같이 직접 도출 할 수 있습니다. 조건부 확률의 비율 정의로 시작하십시오.

$P(B|A) = \frac{P(AB)}{P(A)}$

여기서 공동 확률 및 및 의 한계 확률 .$P(AB)$$A$$B$$P(A)$$A$

현재 공식은 참조하지 않으므로 이것의 정의도 적어 봅시다 :$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

이 작업을 수행하는 작은 요령은 (부울 대수가이 모든 것 아래 에 있으므로 를 표시하여 진리표로 쉽게 증명할 수 있음)를 확인하는 것입니다. :$P(AB) = P(BA)$$AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

이제 이것을 에 대한 공식에 슬롯으로 넣으려면 가 왼쪽에 있도록 위 공식을 다시 작성하십시오 .$P(B|A)$$P(AB)$

$P(AB) = P(A|B)P(B)$

그리고 헤이 프레스토 :

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

요점은 조건부 확률을 이런 식으로 회전시키는 것입니다. 증상이있을 때 누군가가 질병에 걸릴 확률을 유추하려고 시도하는 일반적인 예를 고려하십시오. 즉, 증상 이 있음을 알고 있습니다. 그것을 참조하십시오-그러나 우리는 그들이 질병을 가지고 있고 그것을 유추해야하는지 확신 할 수 없습니다. 수식으로 시작하고 다시 작업하겠습니다.

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

따라서 문제를 해결하려면 증상의 사전 확률, 질병의 사전 확률 (즉, 증상 및 질병이 얼마나 흔하거나 드문 지)과 누군가가 알고있는 증상이있을 가능성을 알아야합니다. 질병 (예를 들어, 고가의 시간 소모적 인 실험실 테스트를 통한).

예를 들어, 여러 가지 질병과 증상이있는 경우이 방법보다 훨씬 더 복잡해질 수 있지만 아이디어는 동일합니다. 더 일반적으로, 베이 즈 정리는 원인 (예 : 질병)과 효과 (예 : 증상) 사이의 관계에 대한 확률 이론이 있고 역 추론을해야하는 경우 (예 : 원하는 증상이있는 경우) 종종 나타납니다. 근본적인 질병을 유추하기 위해).

사고의 두 가지 주요 학교는 통계학 입니다.

베이 즈 정리는 후자와 관련이 있으며 이론이 참일 확률이 새로운 증거에 의해 어떻게 영향을 받는지 이해하는 방법으로 볼 수 있습니다. 이것을 조건부 확률이라고합니다. 수학을 다루기 위해 이것을 볼 수도 있습니다 .

매우 직관적 인 통찰력을 제공하겠습니다. 동전을 10 번 던지고 머리 8 개와 꼬리 2 개가 있다고 가정합니다. 당신의 마음에 떠오르는 질문은이 동전이 머리쪽으로 편향되어 있는지 아닌지입니다.

이제 기존의 정의 또는 잦은 확률 접근 방식을 따르면 동전이 편견이 아니며 이것이 예외적이라고 말할 수 있습니다. 따라서 다음 던지기 가능성도 50 %라고 결론을 내릴 수 있습니다.

그러나 당신이 베이지안이라고 가정하십시오. 실제로 당신은 매우 많은 수의 머리를 가지고 있기 때문에 동전은 머리쪽으로 편향되어 있다고 생각할 것입니다. 이 가능한 편향을 계산하는 방법이 있습니다. 당신은 그것들을 계산하고 다음에 동전을 던질 때 분명히 머리를 부를 것입니다.

따라서 베이지안 확률은 관찰 한 데이터를 기반으로 개발한다는 믿음에 관한 것입니다. 나는 그것이 충분히 간단했으면 좋겠다.

베이 즈 정리는 확률과 가능성이라는 두 가지 아이디어와 관련이 있습니다. 확률은 말한다 :이 모델이 주어진 결과는 다음과 같습니다. 그래서 : 공정한 동전이 주어지면, 나는 시간의 50 %를 얻을 것입니다. 가능성은 말합니다 : 이러한 결과를 고려할 때, 이것이 우리가 모델에 대해 말할 수있는 것입니다. 따라서 : 동전을 100 번 던지고 88 개의 머리를 얻으면 (이전 예에서 픽업하여 더 극단적으로 만들 수 있음) 공정한 동전 모델이 정확할 가능성은 그리 높지 않습니다.

베이 즈 정리를 설명하는 데 사용되는 표준 사례 중 하나는 질병에 대한 테스트 아이디어입니다. 인구의 10000 명 중 1 명이있는 질병에 대해 95 % 정확한 테스트를 수행하고 긍정적 인 테스트를하면 기회는 무엇입니까 그 병에 걸렸다 고?

순진한 대답은 95 %이지만 10000 명 중 9999 명에 대한 테스트의 5 %가 잘못된 긍정을주는 문제를 무시합니다. 따라서 질병에 걸릴 확률은 95 %보다 훨씬 낮습니다.

"기회가 무엇인가"라는 모호한 문구를 사용하는 것은 의도적입니다. 확률 / 우측 언어를 사용하려면 : 테스트가 정확할 확률은 95 %이지만, 알고 싶은 것은 질병이있을 가능성입니다.

약간 벗어난 주제 : Bayes 정리가 모든 교과서에서 해결하는 데 사용되는 또 다른 고전적인 예는 Monty Hall 문제입니다. 퀴즈 쇼에 있습니다. 세 문 중 하나 뒤에 상이 있습니다. 당신은 문 하나를 선택합니다. 호스트는 3 번 문을 열어 상을 공개하지 않습니다. 기회가 주어지면 문 2로 바꾸어야합니까?

나는 질문의 문구를 좋아한다 (아래 참조의 호의) : 당신은 퀴즈 쇼에 있습니다. 백만 개의 문 중 하나에 배상이 있습니다. 당신은 문 하나를 선택합니다. 호스트는 문 104632을 제외한 다른 모든 문을 열어 상을 공개하지 않습니다. 문 104632로 변경해야합니까?

베이지안의 관점에서 베이 즈의 정리에 대해 가장 많이 언급 한 제가 가장 좋아하는 책은 David JC MacKay의 "정보 이론, 추론 및 학습 알고리즘"입니다. 이 책은 Cambridge University Press 책, ISBN-13 : 9780521642989입니다. 제 답변은이 책에서 이루어진 토론의 종류입니다. (일반적인 규칙이 적용됩니다. 저자와 제휴 관계가 없으며 책을 좋아합니다).

가장 명백한 형태의 베이 즈 정리는 단순히 두 가지를 다시 언급 한 것입니다.

1. 관절 확률은 인수 에서 대칭입니다.$P(HD|I)=P(DH|I)$
2. 곱셈 규칙$P(HD|I)=P(H|I)P(D|HI)$

따라서 대칭을 사용하여 :

이제 양쪽을 로 나눌 수 있습니다 .$P(D|I) \neq 0$$P(D|I)$

이게 다야? 어떻게 그렇게 단순한 것이 그렇게 훌륭 할 수 있습니까? 대부분의 것들과 마찬가지로 "목적지보다 더 중요한 여정". 베이 즈 정리는 그것을 이끌어내는 논쟁 때문에 흔들린다.

여기서 빠진 것은 제품 규칙과 합 규칙 은 일관된 추론의 공리를 바탕으로 연역 논리를 사용하여 도출 될 수 있다는 것입니다.$P(H|I)=1-P(\overline{H}|I)$

이제 연역 논리의 "규칙"은 "A는 B를 의미합니다"라는 관계가있는 경우 "B는 A를 의미하지 않음"을 의미합니다. 따라서 우리는 "일관된 추론이 베이 즈 정리를 암시한다"고합니다. 이것은 "베이 베이 즈 정리가 일관성없는 추론을 의미하지 않음"을 의미합니다. 즉, 결과가 이전 및 가능성에 대한 베이지안 결과와 일치하지 않으면 일관성이없는 추론입니다.

이 결과를 콕스 정리라고하며 1940 년대 "유추 대수의 대수"에서 입증되었습니다. 보다 최근의 도출은 확률 이론 : 과학의 논리에서 제공됩니다.

나는 Kevin Murphy의 Bayes Theorem 소개를 정말 좋아합니다. http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html

여기 인용문은 경제학자 기사에서 발췌 한 것입니다.

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

베이지안 접근법의 본질은 새로운 증거에 비추어 기존의 믿음을 어떻게 바꿔야 하는지를 설명하는 수학적 규칙을 제공하는 것입니다. 다시 말해, 과학자들은 새로운 데이터를 기존 지식이나 전문 지식과 결합 할 수 있습니다. 정식 예는 조숙 한 신생아가 첫 번째 일몰을 관찰하고 태양이 다시 떠오르는 지 궁금해하는 것입니다. 그는 가능한 결과에 동일한 사전 확률을 할당하고 하나의 흰색과 검은 색 대리석을 가방에 넣음으로써이를 나타냅니다. 다음 날, 해가 뜨면 아이는 가방에 다른 흰색 대리석을 넣습니다. 가방에서 무작위로 뜯어 낸 대리석이 흰색 일 확률 (즉, 미래의 일출에 대한 어린이의 신뢰도)은 절반에서 2/3로 떨어졌습니다. 다음 날 일출 후 아이는 또 다른 백색 대리석을 추가하고 확률 (따라서 믿음의 정도)은 3 분의 2에서 3 분의 3으로 증가합니다. 등등. 점차적으로, 태양이 매일 아침 떠오르지 않을 것이라는 초기의 신념은 태양이 항상 떠오를 것이라는 거의 확실해 지도록 수정됩니다.