큐브를 구체로 바꾸는 방법은 무엇입니까?

article 기반으로 쿼드 구를 만들려고하는데 다음과 같은 결과가 표시됩니다.

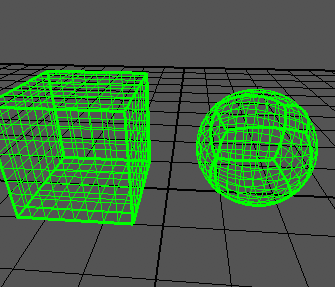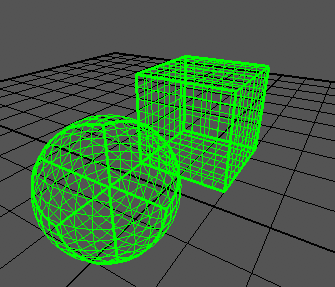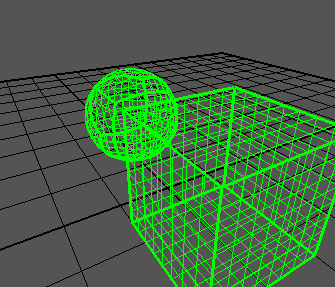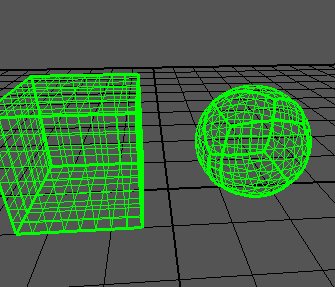
큐브를 올바르게 생성 할 수 있습니다.

그러나이 공식에 따라 모든 점을 변환하면 (위의 페이지에서) :

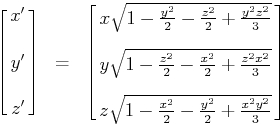
    x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
    y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
    z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

내 구는 다음과 같습니다

보시다시피, 큐브의 가장자리가 여전히 너무 튀어 나옵니다. 큐브 는 기사에서 말하는 것처럼 모든 축 에서 범위에 이르기 -1까지 +1다양합니다.

어떤 아이디어가 잘못 되었습니까?

공식을 잘못 썼습니다.

x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

원본을 수정 x하고 덮어 씁니다. 그런 다음 y원본이 아닌 수정 된 내용을 기준으로 x수정 x합니다. 그런 다음 두z 버전의 수정 된 버전을 기반으로 수정 합니다.

원본을 보존하고 이것을 계산하십시오.

float dx = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
float dy = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
float dz = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

그때부터 dx, dy 및 dz를 사용하십시오.